Social Networks Worksheet

class: center, middle, inverse, title-slide

# Social Networks Worksheet
### Mathew Kiang
### 3/6/2017

---

class: center, middle
# Download the code.red[*]
## [https://git.io/vy8vG](https://git.io/vy8vG)

# Also download the data
## [https://git.io/vy8vO](https://git.io/vy8vO)

---
class: center, middle

# Question 1: Import a network, plot it, plot the degree distribution

---
## Import a network

```r
## Load the libraries (install if necessary)
library(network)
library(tidyverse)
source('./code/network_practical.R')

## Load up data (make sure you have the right file path)
mat1 <- read_csv('./data/unnamed_contact_network.csv', trim_ws = TRUE)

## Convert the matrix into a network
net1 <- as.network(mat1, directed = FALSE)
```

---
## Take a look at the data

```r
print(mat1)
```

```
## # A tibble: 82 × 2
##    Names Contacts
##    <int>    <int>
## 1      1       31
## 2      1       65
## 3      2       61
## 4      2       65
## 5      3       10
## 6      4       16
## 7      5       16
## 8      6       44
## 9      7       44
## 10     8       16
## # ... with 72 more rows
```
---
## Plot the network

```r
## Take a look at the network
plot(net1, label = network.vertex.names(net1))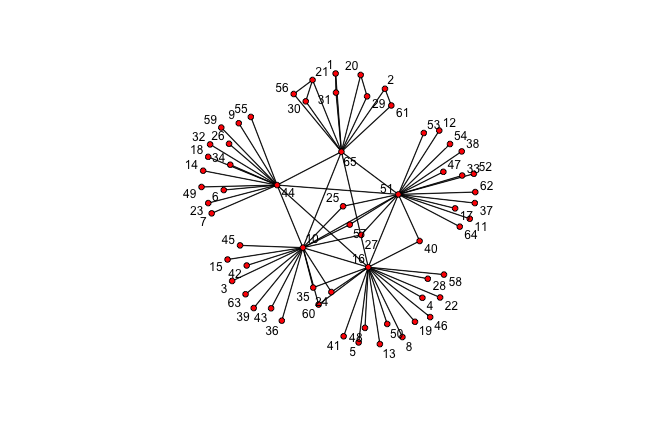
```

![](index_files/figure-html/unnamed-chunk-4-1.png)

---
## Plot the degree distribution

```r
deg <- NULL
for(i in 1:network.size(net1)) {
    deg <- rbind(deg, length(get.neighborhood(net1, i))) 
}
hist(deg)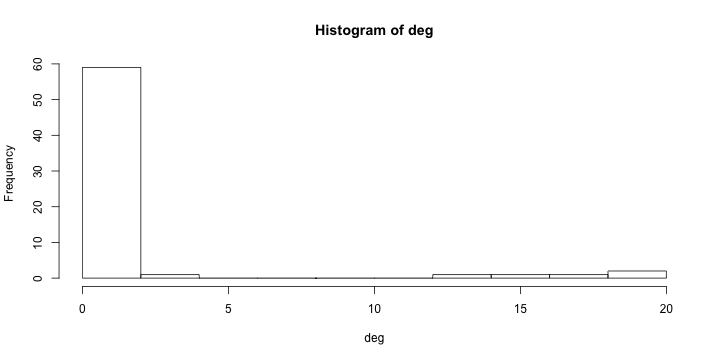
```

![](index_files/figure-html/unnamed-chunk-5-1.png)

---
class: center, middle

# Visualizing randomness
---
## 500 simulations plotted

```r
## This just loops through n_sims times and makes that many lines/simulations
## NOTE: There's a difference between matplot and matlines
n_sims <- 500
for (i in 1:n_sims) {
    sim <- networkPractical(net1, .2, .2, runTime = 50)
    ## If it is the first simulation, we need to create the plot canvas
    if (i == 1) {
        matplot(sim$timeSeries, lty = 1, type = "l", xlim = c(0, 50), 
                ylim = c(0, network.size(net1)), col = alpha(1:3, .15))
    ## If it is not the first one, we just draw on top of the existing canvas
    } else {
        matlines(sim$timeSeries, lty = 1, type = "l", col = alpha(1:3, .15))
    }
}
```

Play with the parameters and see how this affects the plots.

---
## 500 simulations plotted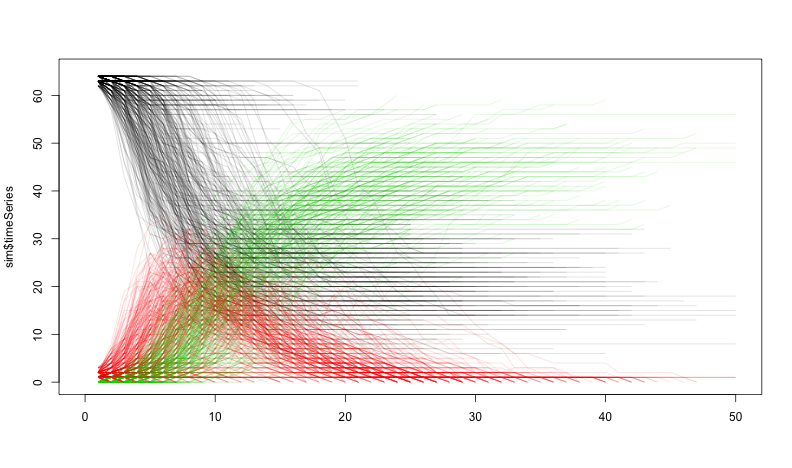
![](index_files/figure-html/unnamed-chunk-7-1.png)

---
class: center, middle
# How does the starting infectious person change our model?

---

## Plot the network

```r
vert_cols <- rep("black", network.size(net1))
vert_cols[c(7, 10)] <- c("green", "red")
plot(net1, label = network.vertex.names(net1), vertex.col = vert_cols)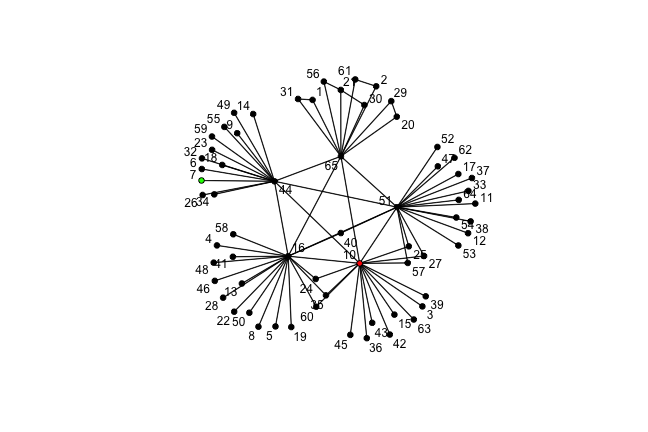
```

![](index_files/figure-html/unnamed-chunk-8-1.png)

Let's plot Node 7 (green) vs Node 10 (red). Note that Node 7 has only one edge, while Node 10 has 18.

---

## Node 7 (green) vs Node 10 (red)

```r
n_sims <- 2000
for (i in 1:n_sims) {
    sim <- networkPractical(net1, .2, .2, runTime = 50, start_infected = 7)
    sim2 <- networkPractical(net1, .2, .2, runTime = 50, start_infected = 10)
    ## If it is the first simulation, we need to create the plot canvas
    if (i == 1) {
        matplot(sim$timeSeries[, 2], lty = 1, type = "l", xlim = c(0, 50), 
                ylim = c(0, 40), col = alpha(3, .03))
        matlines(sim2$timeSeries[, 2], lty = 1, type = "l", 
                 col = alpha(2, .03))
    ## If it is not the first one, we just draw on top of the existing canvas
    } else {
        matlines(sim$timeSeries[, 2], lty = 1, type = "l", col = alpha(3, .03))
        matlines(sim2$timeSeries[, 2], lty = 1, type = "l", 
                 col = alpha(2, .03))
    }
}
```

Modified the loop from before so that now we run two simulations -- one starting on Node 7 (green lines) and one starting on Node 10 (red lines). We plot only the infectious curve.

---
## Node 7 (green) vs Node 10 (red)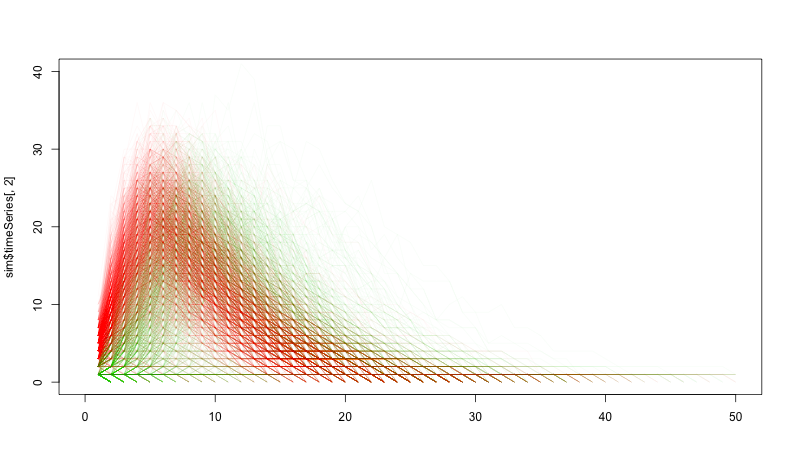
![](index_files/figure-html/unnamed-chunk-10-1.png)

What does the variation between the two colors tell you? What does this imply for network structure and infectious diseases?
---

class: center, middle, inverse
# That's it.
## Thanks