class: center, middle, inverse, title-slide # Utilizing Panel & Repeated Observation Data ## ITAM Short Workshop ### Zhe Zhang, Mathew Kiang, Monica Alexander ### March 16, 2017 --- # Review So Far - Emphasis on "linear" regression - Lots of potential bias, specifically OVB - Conditional independence assumption (CIA) ("controls") - Instrumental variables can generate (local) meaningful variation to study This lecture: using **repeated** observations and time series to get meaningful variation idea is simple, execution is trickier --- # Key Idea 1. with time, there comes "before" and "after" 2. treatment has meaningful variation across places (or times) ??? basically, a carefully thought out version of "*before-and-after*" comparing trends --- # Examples of Panel/Longitudinal Data - neighborhood rent prices over time - Facebook activity for users over time - purchasing activity at Amazon or chain store over time - physical activity measured over time - government-tracked records over time - lots of other cool examples... (today, easier to get time series data) --- # Fixed Effects Imagine that we're looking at 50 islands between 2000 - 2015. What is the effect of the introduction of satellite internet (e.g. at different times)? Our attempt: `$$\log (Earnings_{it}) = \alpha + \delta_t + \gamma Internet_{it} + \beta_1 AvgTemp_i + \beta_2 Beaches_i + \epsilon$$` -- True Value: `$$\log (Earnings_{it}) = \alpha + \delta_t + \gamma Internet_{it} + IslandSpecialty_i + \epsilon_i$$` -- Use fixed effects to capture time-invariant island-specific attributes: `$$\log (Earnings_{it}) = \alpha_i + \delta_t + \gamma Internet_{it} + \epsilon_i$$` *Idea: islands naturally earn different earnings, but using FE, identified using "before" data, we can look at the additive boost from Internet access* ??? First, we'll look at fixed effects Idea here is that islands have specific attributes that are hard to capture adequately like history, building, culture, ease of access. If we argue that these are fixed and how they affect island earnings are constant over time. --- # Introduction to Fixed Effects `$$E[Y_{0i}|X_i,t,\alpha_i,T_i] = E[Y_{0i}|X_i,t,\alpha_i]$$` `\(\alpha_i\)` instead of `\(\{ \alpha_{it}, \alpha \}\)`. Random treatment outcomes, conditional on an individual's *time-invariant unobservables* and *time-varying observables* is still vital; uncorrelated with potential outcomes. - *"as good as randomly assigned"* - individual FE controls some of the potential outcomes **Linear additive model assumption is crucial to the estimation** --- # Estimating FE Models Simply take the average for each person! `\(Y_{i,true} = \alpha_i + \beta X_{it} + \epsilon\)` - since `\(\alpha_i\)` is time-invariant, it should not change across time periods. - estimate individual specific mean `$$\bar{Y}_i = \alpha_i + \gamma \bar{T}_i + \beta \bar{X}_i$$` <br/> 1. demean observations 2. take differences between time-periods --- # FE Concept is General Can include time and region FE too `$$\log (Earnings_{ijkt}) = \alpha_i + Region_j + Firm_k + Year_t + \gamma T_{ijkt} + \epsilon_{ijkt}$$` This is a loose approximation of a time-series model - capturing overall variation over time or time trends - capturing general, wider regional trends --- # Fixed Effects Review - unable to observe data on IQ, ability, motivation, parental influence, etc. --- and we worry it affects potential outcomes (with and without treatment) -- - however, we may argue that this is constant over time --- and FE helps estimate `\(Y_{0i}\)` -- - if so, then we can remove this constant using time series data and only look at deviations from that individual-constant -- **example**: effect of union status on worker wages, using worker specific fixed effects to control for ability (using panel data on worker wages and union status over time) Consider workers who move between companies with and without union wages. Or consider CEOs who move between companies. Or consider using a family fixed effect to control for twins studies. Or consider fixed effects for businesses that work in different sectors. *with time series data, we almost always try to include unit-specific fixed effects if possible* --- # Diff-in-Diff Fixed effects are helpful, but not enough. They can address individual, time-invariant OVB. Sometimes though, there are region or group-wide unobservable variables. Individual fixed effects cannot control for this. Why? ??? Individual FE cannot control for this because things are happening at the broader level to influence the changes -- - The change occurs at the group-level, so there are group-specific unique aspects and differences. -- ### Answer --- *(1) group-specific fixed effects and (2) adequate control group* *Assumes that* - group-level (unobservable) differences are also time-invariant. - Any time-specific effects are equal (and additive) across groups. --- # Diff-in-Diff **Example**: employees all working for companies in state A receive a higher minimum wage **Example**: mobile apps across 4 platforms and across time, studying platform differences **Example**: effect of a product change across states *How could we estimate a causal effect* -- We need to replicate an experimental setting again! - Find an adequate control group. - Estimate a defendable counterfactual / trend without treatment. --- # Diff-in-Diff Graphically  .footnote[ref: Mostly Harmless Econometrics] --- # DiD Example:  .footnote[ref: Mostly Harmless Econometrics] --- # Brief Math Overview of DiD Consider studying fast-food restaurants. Naive (ignores natural group-level differences): `$$Y_{it} = \alpha_i + \delta_t + Post_{it} + \beta X_{it} + \epsilon_{it}$$` -- Use **group-specific FE** and **interaction effect** for a diff-in-diff: `$$Y_{it} = \alpha_i + \delta_t + Post_{it} + \delta TreatedRegion_{i} + \gamma TreatedRegion_{i}\cdot Post_{it} + \beta X_{it}$$` ??? In the first setup, we control for individual level fixed effects and time fixed effect trends. We look at the post-treatment time period for the treated group. However, this suffers from the fact that the --- # Parallel Trend is a Must  .footnote[ref: Todd Gormley slides] --- # Parallel Trend is a Must  .footnote[ref: Todd Gormley slides] ?? Idea is that you use the non-treated group to estimate the counterfactual estimate --- # What are conceptual problems with DiD? -- - non-parallel trend - i.e. local-specific time trends, time shocks - "time varying omitted variables" -- - group-specific unobserveds? OK - time-specific unobserveds? OK -- - Issue: unobserved variables are correlated with both the self-selection of treatment and the timing of the treatment - *example:* individual income boost leads to adoption - *example:* what if group demographics/fundamentals change as a function of treatment? - "avg treatment effect on treated" --- # DiD Example Discussion Bertrand and Mullainathan (2003) looks at state-by-state differences in rules surrounding mergers & acquisitions. DiD = wage differences across states pre-law change and post-law change. *Concerns:* 1. Laws were changing when wages were growing nationally 2. States that choose to change regulation had more unions. ??? Unions have higher wages, so this is accounted for in time-invariant differences States with unions have may time-varying growth trends though, so some self-selection in treatment here. --- # Improve on the Simple Diff-in-Diff Idea Relative time indicators -- - allows the use of variable post-treatment time periods - allows the estimation of dynamic treatment effects - more **robust** to the risk of location-specific time-varying omitted variables .center[<img src = "./assets/DiD_nagaraj_relative_time.png" height = "350">] .footnote[ref: Nagaraj 2017] --- # Improve on the Simple Diff-in-Diff Idea Use matching to limit the control group: - synthetically enforce parallel trends before treatment .center[<img src = "./assets/whole_core_sample_fooddrink.png" height = "350">] .footnote[ref: Zhang Li 2017] --- # Improve on the Simple Diff-in-Diff Idea Use matching to limit the control group: - synthetically enforce parallel trends before treatment .center[<img src = "./assets/basicmatch_metroA_allCities_perUser.png" height = "350">] .footnote[ref: Zhang Li 2017] --- # Checking the Matching Support .center[<img src = "./assets/propensity_density.png" height = "350">] .footnote[ref: Zhang Li 2017] --- # Self-Selection Bias is Always a Concern - under FE, how can we control for the choice to adopt union membership? - under a DiD, how can we control for the state or business choosing to adopt a policy? --- # Improve on the Simple Diff-in-Diff Idea Dig more into the argued causal mechanisms - show that effect is stronger for groups where the theory says it should - e.g., types of companies across states - e.g., categories of purchases across companies **falsification tests** - broader, general idea - pretend that treatment occurs in treated groups before actual treatment. Do we estimate an effect when it should not be there? --- # Private Impact of Public Maps (Nagaraj, 2017) **What is the impact of public goods on private revenues?** - e.g. Wikipedia, Yelp, various online circumstances, Large Hadron Collider, Human Genome Project - In this case: government-provided detailed maps on gold-mining revenues - Do these public goods just replicate private knowledge? *ideas on how to identify the impact?* -- Identification strategy: - variation in available timing of maps - variation in available timing of "non-cloudy" maps - variation in the estimated effect that matches theorized mechanism (theory!) --- # Nagaraj (2017) Diff-in-Diff `$$Y_{it} = \alpha_i + \gamma_1 Post_{it} + \delta_t + \epsilon_{it}$$` *Note: time indicators help remove fluctuations in gold price* *Note: Earth = 9493 blocks* *Note: clustered standard errors at the block level; additional robustness includes more general standard error clustering for spatial proximity* *Note: negative-binomial model also used for robustness* .footnote[ref: Nagaraj 2017] --- # Nagaraj (2017) Diff-in-Diff 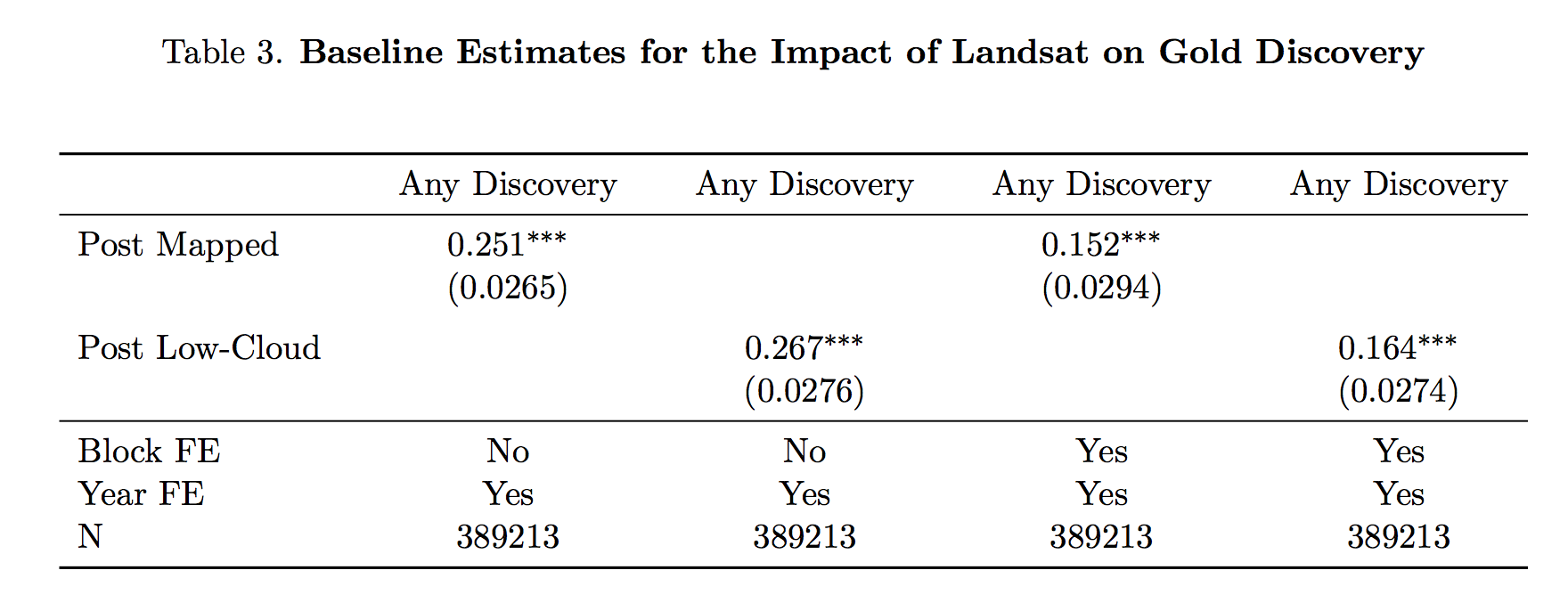 .footnote[ref: Nagaraj 2017] --- # Nagaraj Time-Varying Estimates `$$Y_{it} = \alpha + \sum_{z} \beta_t 1 _{\left\{ z \right\}} + \gamma_i + \delta_t + \epsilon_{it}$$` - Shows no pre-existing differences in trends between blocks (before mapping, whenever it occurred) - Large and persistent effects of discovery over time relative to unmapped places - `\(\sim\)` 7 year lag for the benefits to accrue --- # Nagaraj Time-Varying Estimates .center[<img src = "./assets/DiD_nagaraj_relative_time.png" height = "450">] --- # Nagaraj IV Estimates IV = the probability of receiving a low-cloud cover, high quality mapping. DiD has a concern that the blocks mapped early are not random. .center[<img src = "./assets/nagaraj_iv_checks.png" height = "450">] .footnote[ref: Nagaraj 2017] --- # Nagaraj IV Estimates 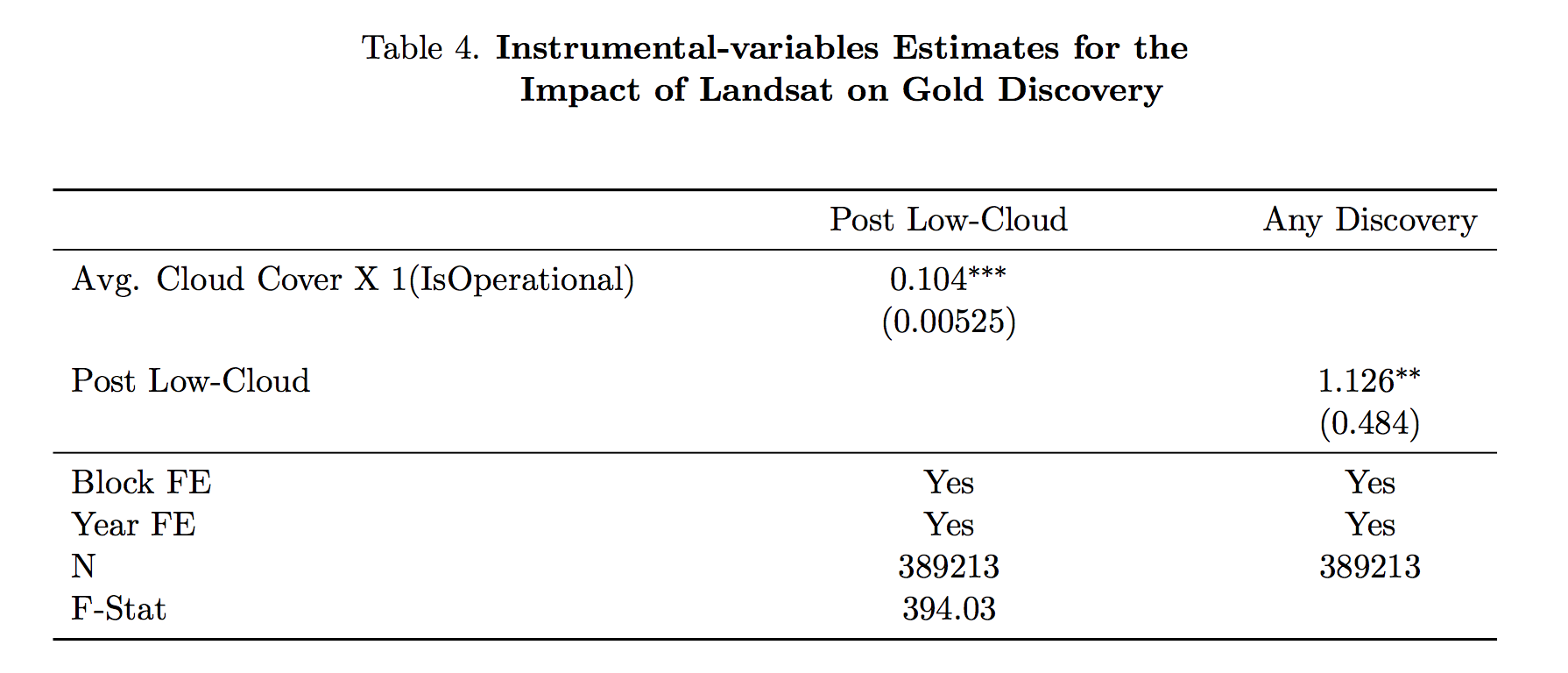 **Why is this so much larger? LATE?** .footnote[ref: Nagaraj 2017] --- # Nagaraj Additional Robustness - Excluding certain regions, like USA or USSR regions. - Removing some of the early blocks, only using variation in blocks mapped later - Placebo test: Estimating Landsat mapping impact on high tree-cover blocks (theory should show no effect) - Placebo test: Randomizing fake mapping dates across blocks. - Removing time dimension and using cross-sectional data only (using delay in mapping as the treatment effect of interest) -- Theory Robustness: - Shows that the effect is MUCH larger for small independent gold firms, than for larger firms, who could be expected to have better mapping investments. - Shows that small, new independent firms are even better off in places with high property rights and low corruption levels. <br/> *Mapping encourages new, smaller entrants; reducing the fixed cost* --- # Hands-On Examples Schooling & Wages Data (Angrist, Kreuger 1991): <http://goo.gl/fGVelu> NJ/PA Min Wage Data (Card, Kreuger 1993): <https://www.dropbox.com/s/j6efjp030znl1aq/minwage.csv?dl=0> <http://masteringmetrics.com/wp-content/uploads/2014/12/Pischke-PS-for-MM.pdf> --- # Sources - Mostly Harmless Econometrics, book - Mastering Metrics, book - Todd Gormley, online slides - Abhishek Nagaraj, "The Private Impact of Public Maps— Landsat Satellite Imagery and Gold Exploration"